Another popular unsupervised machine learning algorithm is K-mean clustering analysis. It is also useful for customer or market segmentation. One of the advantages of using the K-mean clustering method over hierarchical clustering is the ability to work with large dataset. However, K-mean clustering requires you to specify the number of clusters before you perform the analysis, and it only works with numerical data type. The following graph is the normal steps for performing the K-mean clustering analysis.
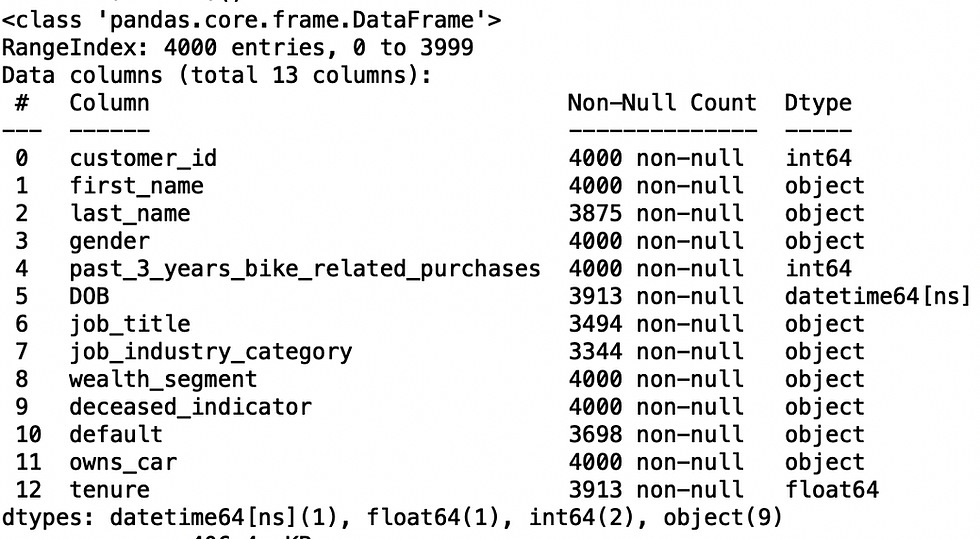
The dataset I use is about a subscription of one telecom company. There are totally 100 observations and 6 columns. The data type is all continuous data, except the Unsubscribe column. R is the programming language for this project.
The normal steps for K-mean clustering is to set the k value first, but I will directly use elbow method to identify the ideal value for me.
library(factoextra)
library(tidyverse)
library(gridExtra)
library(cluster)
library(dplyr)
library(tibble)
# standardize the data with z score
tel_stand <- scale(telecom[ ,2:5])
# we can get the optimal value by using elbow method
set.seed(123)
f <- fviz_nbclust(tel_stand, kmeans, method = "wss")
# it seems that k=4 or 5 is the best, let's say k=4
set.seed(12)
k_mean4 <- pam(tel_stand,k=4)
summary(k_mean4)
plot(k_mean4)
From the silhouette plot, we can see that the overall clustering configuration is not too bad, which is 0.34. Cluster 2 has the best configuration, then cluster 1 , 3, and 4. Cluster 4 is the worst and it has 2 negative observations of silhouette widths.
From the clusplot, we can see that we have 4 clusters. because we can not plot a two-dimensional graph based on the four variables, we use PCA in order to plot the clusters onto a two-dimensional graph with the first two PCS. The first two PCS explains 81.62% of the variations in the dataset, which is decent amount of data.
# let's try k=5
set.seed(12)
k_mean5 <- pam(tel_stand,k=5)
summary(k_mean5)
Because we receive lower average silhouette width than when we use k=4, therefore we forsake k=5. Let's stick to k=4.
# find out the numbers of each cluster
length(which(k_mean4$silinfo$widths[ ,1] ==1))
length(which(k_mean4$silinfo$widths[ ,1] ==2))
length(which(k_mean4$silinfo$widths[ ,1] ==3))
length(which(k_mean4$silinfo$widths[ ,1] ==4))
39,33,12,16 are the numbers of each cluster
# put the medoids with sum cluster together
newdata10 <- add_column(as.data.frame(k_mean4$medoids),
Cluster_number = c(39,33,12,16),
.before= 1)
The characteristics of each cluster:
Cluster 1: total 39 customers, relatively younger, lower income, lower usage of the service, and shorter tenure in the company.
Cluster 2: total 33 customers, youngest, lowest income, lowest usage of the service, and shortest tenure in the company.
Cluster 3: total 12 customers, oldest, highest income, highest usage of the service, and longest tenure in the company.
Cluster 4: total 16 customers, relatively older, higher income, higher usage of the service, and longer tenure in the company.
Based on the traits of the clusters, the company can use different marketing activities to promote to each group of customers. Or the company can even go deeper to each group of customers and to cluster them again in order to gain more insight from the data.
So now I want to know the percent of customers that have unsubscribed to the service from each cluster.
# put each assigned cluster number to the tel_stand dataset (after scaled)
telecom$cluster <- k_mean4$clustering
new <- telecom %>%
group_by(cluster) %>%
summarise(mean_unsubscribe = mean(Unsubscribe))
Based on the output, the percent of unsubscribers of cluster 1 is 46.2%, cluster 2 is 93.9%,cluster 3 and 4 is 0%, respectively.
The company may need to focus on cluster 2, then 1 in order to keep them to the service. Recall that the traits of cluster 2 are youngest, lowest income, lowest usage and shortest tenure. It is possible because the service provided by the company can't meet the young people's needs, or because the service is too expensive to afford for them. There are so much insight we can get from the output.
Comments